Philips – A New Ray-tracing Method for Non-imaging Optics #SWI2012

Introduction

In illumination engineering, the transfer of light from the source to the target is computed to obtain photometric quantities like the luminous intensity, color point, and brightness. The technique that is commonly used is the Monte Carlo (MC) ray tracing method that traces randomly rays through an optical system containing components like lenses and mirrors. To determine for example the illuminance and intensity on a target area for a given optical system, typically 10,000 to 1,000,000 rays need to be traced from the source to the detector which makes this method quite expensive. This becomes, even more, a problem when this technique is used to optimize the design or when color parameters are needed. Moreover, although the MC technique is a robust method and widely applied in the industry it suffers inherently from computational noise.

Problem formulation

An idea to speed up the computations is based on the edge-ray principle as described in [1,2]. A ray at a surface can be described by 2 spatial and 2 direction coordinates, which define a four-dimensional space. Ray tracing can therefore be interpreted as a numerical technique to map the phase space of the light at one surface into another surface.

The phase space on the target can be partitioned into sets of rays according to their path through the optical system. It is proven [1] that all rays in one set at the source will remain in this set at the target. Therefore, it is enough to determine the boundaries of the ray sets and the density within the sets to obtain the photometric data at the target. This technique will require fewer rays to be traced and will result in more accurate data, especially in the areas with a low illuminance, when compared with tracing a large number of random rays. Consequently, the CPU time can be reduced significantly.

Questions

• What would be an efficient algorithm to determine the edges of the ray sets on the target?
• Given the edges, what would be an efficient algorithm to determine the flux density within a ray set?
• What would be performance gain compared with a classical MC approach?

Considering the available time we would propose to limit a practical implementation to one space and one-directional coordinate.

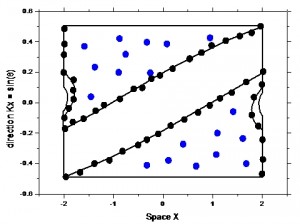
Figure 1, The 2D phase space of a compound parabolic collimator at the exit face.

[1] H. Ries and A. Rabl, Edge-ray principle of nonimaging optics, J. Opt. Soc. Am. A, pp. 2627-2632, 1994.

[2] R. Winston et al, Nonimaging Optics, Elsevier Academic Press, 2005, ISBN 0-12-759751-4