PostNL – Model for Optimal Connection Between Customer and Sorting Center #SWI2020
Apart from mail delivery, PostNL’s most important service is to transport parcels ordered at webshops (PostNL’s customers) to consumers. This service is provided at an enormous speed and accuracy (99% within 24 hours) and at incredibly high volumes (parcels per day). As a consequence, highly efficient business processes are required to maintain this service in a cost-effective way. Moreover, PostNL is constantly reinventing its logistic organization to keep up with the enormous increase of parcel volumes and the ever-changing preferences of consumers.
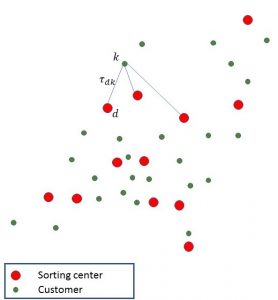
The PostNL process for transporting parcels from webshops to consumers is subdivided into separate processes that can be studied and optimized more or less independently: collection, first sorting (to the level of rough destination area), transport (cross-docking), second sorting (to consumer addresses) and distribution from the second sorting center to the consumer. The problem we want to address in the workshop “Mathematics with Industry” is focused on the collection process, and in particular on the optimal connection between customer and sorting center. The problem arises from the regional unbalance of webshops, i.e. most of PostNL customers are located in the south of The Netherlands, whereas the destination locations of the consumers are more concentrated around the big cities. Therefore, it is not efficient to connect each customer simply to its most nearby sorting center because then the southern sorting centers would lack sorting capacity whereas the northern sorting centers would have an overcapacity. Note that the locations of the sorting centers are optimized for the second sorting process, i.e. to facilitate the distribution to consumers.
In general terms, the proposed problem is to find an optimal balance between transportation costs and sorting costs. Thereby, transportation costs are roughly proportional to the travel time between customer and sorting center, whereas sorting costs depend on the number of workforces that need to be hired to do the job in a given time frame. Moreover, the two cost types are mutually related because a later arrival of parcels at a sorting center due to longer transportation times may render the sorting process impossible to accomplish within the time constraints. Nevertheless, such extra transportation and sorting costs may be necessary to prevent capacity overflows at some sorting centers.
Our goal for the workshop is to find a mathematical model for the costs of the collection problem that covers a sufficient amount of detail and at the same time is simple enough to enable a mathematical or numerical approach regarding its minimization. We are also very eager to acquire ideas about mathematical methods for the solution of such models.
Figure 1. Graphical representation of the problem setting.